Producto de vectores
Existen tres tipos de producto en los vectores, y en cada uno de ellos da un tipo de magnitud vectorial o escalar
Producto de un vector por un escalar
Partiendo de la representación gráfica del vector, sobre la misma línea de su dirección tomamos tantas veces el módulo de vector como marque el escalar, que de ser negativo cambia el sentido (ver gráfico).
Partiendo de un escalar n y de un vector a , el producto de n por a es na , es el producto de cada una de las coordenadas del vector por el escalar, representando el vector por sus coordenadas:
Si lo multiplicamos por el escalar n:
Esto es:
Representando el vector como combinación lineal de los vectores unitarios:
multiplicándolo por un escalar n:
esto es:
Hagamos un ejemplo con valores numéricos, partimos del vector:
multiplicamos el vector por 2,5:
esto es:
haciendo la operaciones
"Como se ha observado el producto de un escalar por un vector da como resulatado otro vector"
Propiedades de Producto de un vector por un escalar
El producto de un vector por un escalar cumple las siguientes propiedades:
Siendo u y v vectores y k un escalar
1.- Conmutativa: k • v = v • k.
2.- Distributiva: k (v + u) = (k • v) + (k • u).
3.- Elemento Neutro: 1 • v = v.
4.- Elemento Simétrico: -1 • v = - v.
- Producto Escalar de dos Vectores
La multiplicación da como resultado un número real , no un vector, por lo que esta operación se denomina producto escalar. Al igual que la suma, también puede realizarse de forma matemática y de forma gráfica.
Conociendo el ángulo entre los vectores y el módulo de cada vector tenemos que el producto de escalar de los vectores analíticamente se cálcula:
Conociendo las componentes de los vectores tenemos que el producto de escalar de los vectores en forma algebraica se cálcula:
Vemos que:
Propiedades del Producto Escalar
1. El producto escalar del vector nulo por otro vector cualquiera vale 0.
2. Si dos vectores son perpendiculares, su producto escalar es 0.
3. Si B (a,b) es una base ortonormal, se cumple:
4. Propiedad conmutativa: Si a y b son dos vectores cualesquiera, se verifica:
6. El producto escalar de un vector por sí mismo es igual al cuadrado de un módulo:
“Esta propiedad nos permite calcular el módulo de un vector conociendo el producto escalar del vector por sí mismo”
De las propiedades tenemos que para los vectores unitarios:
Producto Vectorial de dos vectores
El producto vectorial de los vectores a y b, se define como un vector, donde su dirección es perpendicular al plano de a y b, en el sentido del movimiento de un tornillo que gira hacia la derecha por el camino más corto de a a b.
La expresión relaciona al producto vectorial con el área del paralelogramo que definen ambos vectores.
Componentes del producto vectorial de dos vectores

Dirección y sentido del vector resultante del producto vectorial de dos vectores
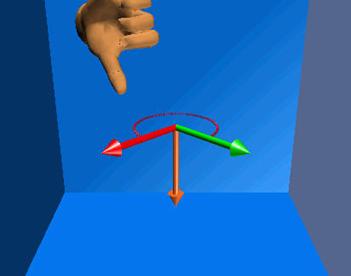
Si determinamos el sentido con la regla de la mano derecha, colocamos los dedos índice, medio, anular y meñique en el sentido del primer factor (en nuestro ejemplo el vector a) y cerramos la mano rotando los dedos antes mencionados el ángulo a. El dedo pulgar queda indicando el sentido del seudo-vector c.
Si aplicamos la regla del tornillo, ubicamos un tornillo perpendicular al plano determinado por los dos factores, y lo giramos en el sentido que se debe rotar el primer factor sobre el segundo para que gire el ángulo a. El sentido que avanza el tornillo, es el sentido del seudo-vector producto c.
Si aplicamos la regla del tornillo, ubicamos un tornillo perpendicular al plano determinado por los dos factores, y lo giramos en el sentido que se debe rotar el primer factor sobre el segundo para que gire el ángulo a. El sentido que avanza el tornillo, es el sentido del seudo-vector producto c.
Propiedades del producto vectorial de dos vectores
1. Anticonmutatividad
2. Para vectores no nulos. Si dos vectores son paralelos su producto vectorial da igual a cero.
3. Distributiva con respecto a la suma
4. La regla de la expulsión.
5. Identidad de Jacobi.
6. El vector unitario es normal al plano que contiene a los vectores a y b .


























Me encanto! Excelente los detalles en cuanto a videos y demas! Sumamente util, felicidades!
ResponderEliminarEn la segunda propiedad del producto escalar aparece que el cos 0°=0
ResponderEliminarsi os0|=1
Eliminaryo tengo una pregunta? que es la algebraica del producto vectorial
ResponderEliminarcallate
Eliminar