Los vectores es uno de los conocimientos de las matemáticas que provienen de la física. En la distingue entre magnitudes escalares y magnitudes vectoriales. Se llaman magnitudes escalares aquellas en que sólo influye su tamaño. Por el contrario, se consideran magnitudes vectoriales aquellas en las que, de alguna manera, influyen la dirección y el sentido en que se aplican.
A estas magnitudes vectoriales se representa por un vector.
Un vector es todo segmento de recta dirigido en el espacio. Cada vector posee unas características que son:
• Origen o también denominado Punto de aplicación. Es el punto exacto sobre el que actúa el vector.
• Módulo: Es la longitud o tamaño del vector. Para hallarla es preciso conocer el origen y el extremo del vector, pues para saber cuál es el módulo del vector, debemos medir desde su origen hasta su extremo.
• Dirección: Viene dada por la orientación en el espacio de la recta que lo contiene
• Sentido: Se indica mediante una punta de flecha situada en el extremo del vector, indicando hacia qué lado de la línea de acción se dirige el vector.
Hay que tener muy en cuenta el sistema de referencia de los vectores, que estará formado por un origen y tres ejes perpendiculares. Este sistema de referencia permite fijar la posición de un punto cualquiera con exactitud.
El sistema de referencia que usaremos, como norma general, es el Sistema de Coordenadas Cartesianas.
Para poder representar cada vector en este sistema de coordenadas cartesianas, haremos uso de tres vectores unitarios.
Estos vectores unitarios, son unidimensionales, esto es, tienen módulo 1, son perpendiculares entre sí y corresponderán a cada uno de los ejes del sistema de referencia.
Por ello, al eje de las X, le dejaremos corresponder el vector unitario o también denominado .
Del mismo modo, al eje Y, le corresponderá el vector unitario o también denominado .
Finalmente, al eje Z, le dejaremos corresponder el vector unitario o también denominado .
Vectores unitarios y componentes de un vector
Cualquier vector puede ser considerado como resultado de la suma de tres vectores, cada uno de ellos en la dirección de uno de los ejes coordenados.
Si consideramos ahora sobre cada eje un vector, aplicado en el origen, cuyo sentido es positivo y cuyo módulo consideramos como unidad de longitudes, podemos sustituir cada uno de los sumandos de la expresión anterior por el producto de un escalar por el correspondiente vector unidad.
De ese modo,
Los escalares α, β, γ se denominan componentes del vector y se representan por:
Los vectores
Son los vectores unitarios y suelen representarse respectivamente por i, j, y k.
También puede representarse de la siguiente forma:
Módulo de un vector
Un vector no solo nos da una dirección y un sentido, sino también una magnitud, a esa magnitud se le denomina módulo.
Gráficamente: es la distancia que existe entre su origen y su extremo, y se representa por:
Coordenadas cartesianas: En muchas ocasiones es conveniente tomar las componentes sobre tres direcciones mutuamente perpendiculares OX, OY y OZ que forman un sistema cartesiano tridimensional.
Si tomamos tres vectores unitarios, i sobre OX, j sobre OY y k sobre OZ, entonces podemos encontrar puntos ax, ay, az sobre OX, OY, OZ, respectivamente, tales que:y aplicando el teorema de Pitágoras nos encontramos con que el módulo de a es:
Tipos de vectores
Según los criterios que se utilicen para determinar la igualdad de dos vectores, pueden distinguirse distintos tipos de los mismos:
• Vectores libres: no tienen su extremo inicial -u origen- fijado en ningún punto en particular.
• Vectores fijos: tienen su extremo inicial -u origen- fijado en algún punto en particular.
• Vectores equipolentes: son vectores que presentan iguales módulos, direcciones y sentidos.
• Vectores deslizantes: son vectores equipolentes que actúan sobre una misma recta.
• Vectores concurrentes: comparten el mismo extremo inicial -u origen-.
• Vectores unitarios: vectores de módulo igual a uno.
• Vectores opuestos: vectores de distinto sentido, pero igual magnitud y dirección (también vectores anti - paralelos)
• Vectores coplanales: vectores que se encuentran dentro del mismo plano
Para completar ir a la página:







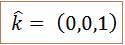










Muchas gracias hermano, tu post me ayudó muchisimo a entender este tema, saludos desde Nicaragua.
ResponderEliminarGracias ssss
ResponderEliminarGracias, este post esa muy completo con una explicación que se entiende a la primera, no como otros. Me ayudó, de nuevo muchas gracias
ResponderEliminar